PÉNDULO SIMPLE

El péndulo simple es uno de los modelos ideales más comunes en la física, consiste en una masa puntual suspendida de un hilo de masa despreciable y que no se puede estirar. Si movemos la masa a un lado de su posición de equilibrio (vertical) esta va a oscilar al rededor de dicha posición.

La plomada de un teodolito y un niño que se balancea en un columpio son ejemplos prácticos que se pueden simular o modelar como un péndulo simple.

Debemos tener en cuenta que para que este modelo sea válido, lasoscilaciones deben ser pequeñas. Esto en razón a que para ángulos pequeños el seno de ángulo Ɵ es casi igual al ángulo Ɵ en radianes.

Así podemos decir que el movimiento del péndulo simple es armónico y que al estudiar la dinámica de su movimiento obtendremos que el periodo y la frecuencia dependen solamente de la longitud y la gravedad.

A continuación vamos a ver un ejercicio sencillo y práctico para entender un poco mejor este concepto. Si te gusto este articulo suscribete al boletín electronico de Mi Profesor de Fisica para que recibas artículos y videos relacionados con otros temas de física general.

VER VÍDEO

Fundamentos físicos

Un péndulo simple se define como una partícula de masa m suspendida del punto O por un hilo inextensible de longitud l y de masa despreciable.

Si la partícula se desplaza a una posición q₀ (ángulo que hace el hilo con la vertical) y luego se suelta, el péndulo comienza a oscilar.

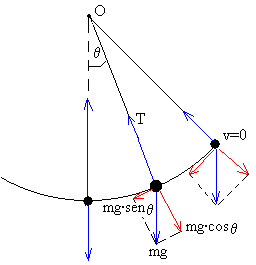
El péndulo describe una trayectoria circular, un arco de una circunferencia de radio l. Estudiaremos su movimiento en la dirección tangencial y en la dirección normal.

Las fuerzas que actúan sobre la partícula de masa m son dos

• el peso mg
• La tensión T del hilo

Descomponemos el peso en la acción simultánea de dos componentes, mg·senq  en la dirección tangencial y mg·cosq en la dirección radial.

• Ecuación del movimiento en la dirección radial

La aceleración de la partícula es a_n=v²/l dirigida radialmente hacia el centro de su trayectoria circular.
La segunda ley de Newton se escribe
ma_n=T-mg·cosq
Conocido el valor de la velocidad v en la posición angular q  podemos determinar la tensión T del hilo.
La tensión T del hilo es máxima, cuando el péndulo pasa por la posición de equilibrio, T=mg+mv²/l
Es mínima, en los extremos de su trayectoria cuando la velocidad es cero, T=mgcosq₀

• Principio de conservación de la energía

En la posición θ=θ₀ el péndulo solamente tiene energía potencial, que se transforma en energía cinética cuando el péndulo pasa por la posición de equilibrio.

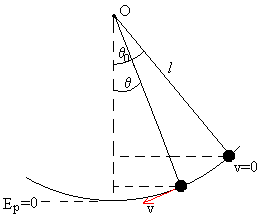
Comparemos dos posiciones del péndulo: En la posición extrema θ=θ0, la energía es solamente potencial. E=mg(l-l·cosθ0) En la posición θ, la energía del péndulo es parte cinética y la otra parte potencial La energía se conserva v2=2gl(cosθ-cosθ0) La tensión de la cuerda es T=mg(3cosθ-2cosθ0) La tensión de la cuerda no es constante, sino que varía con la posición angular θ. Su valor máximo se alcanza cuando θ=0, el péndulo pasa por la posición de equilibrio (la velocidad es máxima). Su valor mínimo, cuando θ=θ0 (la velocidad es nula). Ecuación del movimiento en la dirección tangencial La aceleración de la partícula es at=dv/dt. La segunda ley de Newton se escribe mat=-mg·senq La relación entre la aceleración tangencial at y la aceleración angular a es at=a ·l. La ecuación del movimiento se escribe en forma de ecuación diferencial  (1) Medida de la aceleración de la gravedad Cuando el ángulo q  es pequeño entonces, senq » q , el péndulo describe oscilaciones armónicas cuya ecuación es q =q0·sen(w t+j ) de frecuencia angular w2=g/l, o de periodo La ley de la gravitación de Newton describe la fuerza de atracción entre dos cuerpos de masas M y m respectivamente cuyos centros están separados una distancia r. La intensidad del campo gravitatorio g, o la aceleración de la gravedad en un punto P situado a una distancia r del centro de un cuerpo celeste de masa M es la fuerza sobre la unidad de masag=F/m colocada en dicho punto. su dirección es radial y dirigida hacia el centro del cuerpo celeste. En la página dedicada al estudio del Sistema Solar, proporcionamos los datos relativos a la masa (o densidad) y radio de los distintos cuerpos celestes. Ejemplo: Marte tiene un radio de 3394 km y una masa de 0.11 masas terrestres (5.98·1024 kg). La aceleración g de la gravedad en su superficie es Tenemos dos procedimientos para medir esta aceleración Cinemática Se mide con un cronómetro el tiempo t que tarda en caer una partícula desde una altura h. Se supone que h es mucho más pequeña que el radio r del cuerpo celeste. Oscilaciones Se emplea un instrumento mucho más manejable, un péndulo simple de longitud l. Se mide el periodo de varias oscilaciones para minimizar el error de la medida y se calculan  el periodo P de una oscilación. Finalmente, se despeja g de la fórmula del periodo. 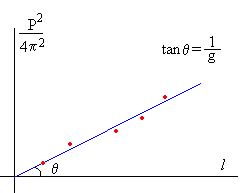De la fórmula del periodo establecemos la siguiente relación lineal. Se representan los datos "experimentales" en un sistema de ejes: P2/(4p2) en el eje vertical y La longitud del péndulo l en el eje horizontal. La pendiente de la recta es la inversa de la aceleración de la gravedad g.